数学内外

Inside and Outside of Mathematics

田 刚

大家好！今天的讲座是今年中国数学会主办的第一个面向公众的在线讲座。今天是母亲节，在此也向天下所有伟大的母亲致以节日的祝福！我的母亲也是一位数学家，她是我数学的第一位启蒙老师，我讲座的题目是数学内外，这个题目的灵感也是来自于我的母亲。在很小的时候她告诉我，数学可以有很多角度去认识它。我们知道在数学专业研究领域之外的人，与进入到数学研究领域的人，所获得的体会和感受是不一样的。下面让我们从各个不同的角度一起了解数学内外的奥秘。

在我国古代，数学叫作算术，是六艺之一。六艺指六种技能：礼、乐、射、御、书、数，其中的“数”就是指算术，也就是数学。六艺源自于中国周朝的贵族教育体系，周王官学要求学生掌握的六种基本才能。有点像我们今天高考一样，即使是文科考生，也要考数学，学数学的也需考语文。

在我国古代，数学叫作算术

大家知道古希腊是西方文明的源头之一，是西方文明最重要和直接的渊源。西方有记载的文学、科技、艺术大都是从古代希腊开始的。当然古希腊不是一个国家的概念，而是一个地区的称谓。数学在古希腊语有学习、学问、科学之意，被认为是“学问的基础”。

数学在古希腊语有学习、学问、科学之意

古希腊数学家普洛克拉斯说：“哪里有数学，哪里就有美。”数字不仅可以展现美，它还可以量化世间万物，让事物变得更有趣。我国著名数学家华罗庚先生说过：“就数学本身而言，是壮丽多彩、千姿百态、引人入胜的…认为数学枯燥乏味的人，只是看到了数学的严谨性，而没有体会出数学的内在美！”数学美是自然美的客观反映，是科学美（内在美）的核心，也体现在艺术等美中。

比如，自然界中的花朵。大家春天都喜欢踏青赏花，在花朵上也能找到数学的影子。比如三角梅有3片花瓣，银莲花有5片花瓣。图片上这朵向日葵，呈现出斐波那契数列，斐波那契数列是从第3项开始，每一项都等于前两项之和。这朵向日葵有21个深蓝色螺旋和13个宝石绿螺旋。13和21是斐波那契数列中的相邻数字。仿佛花朵也有“数学头脑”。

建筑中也有数学。下图是谢克洛弗拉清真寺房顶，建于17世纪的伊朗伊斯法韩，使用了双螺旋图案。它建于1602至1619年阿巴斯一世统治时期，建造工程历时长达17年，用于献给阿巴斯的岳父Sheikh Lotfollah，这个清真寺也用岳父的名字命名，Sheikh Lotfollah是一位受人尊敬的黎巴嫩伊斯兰教学者，应邀来到伊斯法罕监管国王的清真寺和神学院。从高高的窗格射进来的光线会随着阳光的角度不断变化，甚至穹顶上用到的白色瓷砖据说也会在一天里由白色变成粉红，真是非常奇妙。另外，为了保证信徒朝拜的方向对着圣地麦加，设计清真寺时需要经过严密的数学计算。

建于17世纪的伊朗伊斯法韩谢科洛夫拉清真寺的房顶

大家所熟知的画家达芬奇，在他的画中，也能看到大量的数学理念。当然达芬奇为大家所熟知的是他画家的身份，其实他也精通生理解剖、建筑、音乐、以及数学等等，被誉为是全才。著名的数学表达式斐波纳契数列以及其中衍生的“黄金分割”定律，在达芬奇为数不多却闻名于世的绘画作品中反复运用，其中就包括《蒙娜丽莎》和《最后的晚餐》。

《蒙娜丽莎》中体现的黄金分割率

达芬奇《最后的晚餐》

这里我们可以打个比方：数学是一座百花齐放的美丽花园，但它的周围有墙挡着，外边的人不能一下子就领略到它的美丽。如果只是站在门外看，只能看到它通过自然和艺术等表现的美。数学作为科学之母，它的抽象和严谨，也决定了需要有一些基础和投入更多的理解力才能真正感受它更深刻、更美妙的魅力。

下面让我们从数字的起源和早期的一些情况开始探索数学内外的奥秘。

据专家考证，数学起源于人类早期的生产活动，其基本概念的精炼就已出现在古埃及等的古代数学文本内。最早，人类采用实物记数的方法，如用小石头、 树枝等，后来变成在骨片上刻画来计数。随着生产力的发展，后来有了绳子，便出现了结绳计数。我国《易经》中提到了“结绳计数”，在世界其他地方，如印加帝国、希腊、波斯、罗马都有。

公元前8000年左右，人们便开始用陶筹计数作为计数器，后来陶筹被沿用了5000年未曾间断。举个例子来说，当时的羊群所有者如何保证帮他放羊的牧羊人，在很长一段时间的放牧之后，羊群数目能对的上呢？当时的古人使用的是陶筹这样的计数工具。陶筹计数简单来说，就是双方把陶筹包裹在空心泥球里保存，双方在表面签名，以证明其真实性，这样即使是牧羊人放牧了很长一段时间后回来，羊群所有者和牧羊人对一下陶筹与羊群的数量即可，解决了信息不对称的问题。后来人们在表面画出内部样子，就可在不破坏泥球的前提下，知晓内部数量。

陶铸计数

有考古学家认为陶筹与楔形文字的发明有重要关系。再后来随着人们智力的发展和实践活动的不断磨练总结经验，人们意识到不需要实际的陶筹，把筹码数量画在板上即可，就有了泥板。这里要提到的一个古老的民族——苏美尔人。苏美尔人是于公元前5000年左右迁徙到西亚两河流域南部地区居住的一支古老民族。苏美尔人于公元前3000年就进入了文明时期, 创造了人类历史上最早的一个古文明，公元 3400 到公元前 3000 年，苏美尔人的乌鲁克泥板上发现了第一个有记录财务数据的文件。我们从下图显示的泥板中得知：一个叫辛库的财务在37个月中收到29086单位的大麦。

苏美尔人的乌鲁克泥板

起初计数的符号取决于被计数的对象，羊与牛的符号是不一样的。

公元前3千纪初期，数字获得了新的生命形式。为了表示10头牛，人们可以不再画10个牛头，只需写个数字10，旁边画一个牛头。这一刻意味着，数字已经独立存在。数字从具体物品中、从现实中抽离出来，产生了数的概念。这是人类一个最伟大的发明。起初是自然数，如1，2，3，4，5，6，7，8，9，…这些数字我们称为阿拉伯数字，实际上我们现在通用的这种数字书写法是印度人发明的，大约在700年左右，阿拉伯学者在被征服的地区发现当地数学比他们的先进，于是接纳了这套印度数字，阿拉伯世界随后见证了数学的巨大发展，而当时的欧洲人却对此视而不见，仍然使用较为费事的罗马数字。数学家斐波那契是在西方推行印度阿拉伯数字的先行者，一直到13世纪印度阿拉伯计数法才慢慢在西方推广开来，可见开放心态和慧眼识珠的重要性。之后由于实际应用和四则运算，就需要引进有理数，即两个整数的比。古希腊数学家、哲学家毕达哥拉斯是有记载的第一个注重“数”的人，当时他发出感叹说：数是万物之本。数字的抽象化，是一个极其重要的具有划时代意义的节点。

毕达哥拉斯画像

数的概念产生之后，数学逐渐形成独立的学科。早期几何学是关于长度、角度、面积和体积的经验原理，用于满足在测绘、建筑、天文和工艺制作中的实际需要。几何的英文geometry，由词根geo-（大地）加上metry（测量）组成，本意是“测量大地”，最初的几何学就是如何测量土地面积的学问。可以说最初的土地测量员就是 “最接地气”的“数学家”。

土地测量员等早期“数学家”要解决的主要问题包括：如何划分土地面积？如何按照面积计算土地的价格？两块地哪块更接近水源？水渠的修建应该遵守什么样的路线才能使距离最短？等等这些与生产生活紧密相关的问题。

据说治水的大禹是我国最早的测量员之一。战国时期水利家郑国，他主持勘察测量、设计的郑国渠是我国古代四大古渠之一。这其中还有一个有趣的故事，郑国其实是韩国的间谍，他前往秦国游说秦王修筑水利工程，以起到拖累秦国的目的。但没想到，水渠修筑之后，秦国国力因此变得更加强大。虽然郑国未能起到拖垮秦国的目的，但是作为一名卓越的水利专家，郑国治理水患，改变了关中农业区的面貌，值得称颂。这个故事也告诉我们：自强才是御敌之本。

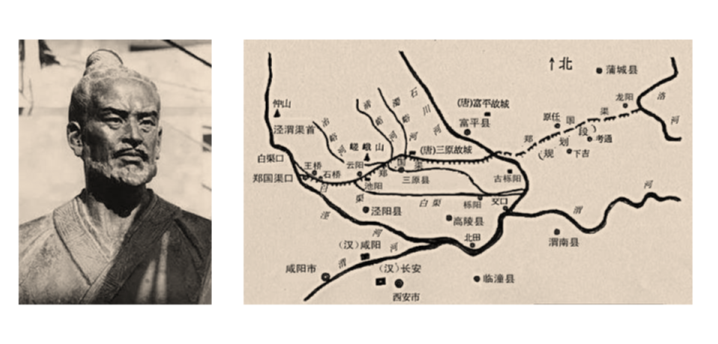
郑国与郑国渠图示

下图中展示了新石器时代的陶罐，上面有很多几何纹饰，这些几何纹饰来源于生产生活，反映了当时社会生活的各个方面，包括图腾崇拜等，也有一种说法是这些陶罐反映了原始人的审美观念已经从实用中分离出来。马家窑文化因最早发现于甘肃省临洮县的马家窑村而得名，年代约为公元前4200年至前3300年，也就是距今五千七百多年的新石器时代晚期。半山文化是马家窑文化的晚期类型之一，因甘肃省广河县（一说是和政县）半山遗址而得名。

新石器时代的陶罐

差不多同期，在公元前3000年，埃及人就有方形棱锥的锥台体积的正确公式。大家熟知的埃及金字塔就是对称、比例精确的三角形。金字塔是由无数裁切准确的巨大石块组成的帝王陵墓，当时的人们把金字塔有条不紊地安置在规矩的空间中，呈现出高度秩序。

古巴比伦与中国、古埃及、古印度一并称为“四大文明古国”。图片中所示的是古巴比伦伊什塔尔城门。这是德国考古学家在发现巴比伦古城时发掘，之后带回了柏林的博物馆。

德国佩加蒙博物馆伊什塔尔城门

古巴比伦时期的数学很发达，计数法采用的是十进位和六十进位法。钉头型代表1，尖头型代表10，通过加法这两个符号可以表示直到59，比如32由3个尖头型和2个钉头型构成。从60开始使用符号组，记录60的符号也是由之前的符号构成，比如数字145由2个60构成120，再加25个单位。六十进位法应用于计算周天的度数和计时，至今为全世界所沿袭。在代数领域，古巴比伦人已经可解含有三个未知数的方程式。另外，古巴比伦人还有一个三角函数表。

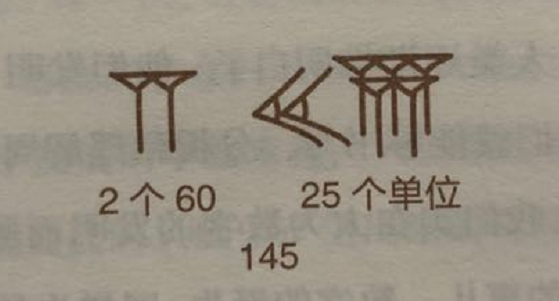
古巴比伦计数法

数学经过初期的发展后，不再局限于田间地头、修筑工程等与农业生产等息息相关的技术，而是逐渐形成了一门研究数量、结构、变化、空间等概念的学科。数学形成学科之后，越发突显这样的几个特点：数学的指向是现象背后的客观规律，它是抽象的，严密的逻辑是其基础。数学追求的是抽象美和终极真理。它逻辑性强并以兴趣和好奇心为首要驱动。数学非常纯粹，它的正确与否不因人的意志而改变。

世界上比较早地用严密逻辑探讨世界本源的发端之一是意大利半岛的古希腊。柏拉图学园门口挂着“不懂几何者，不得入内。”当时的几何，即是指数学。下图是意大利著名画家拉斐尔的《雅典学园》取材于公元前4世纪古希腊哲学家柏拉图举办柏拉图学园的故事，整幅画洋溢着浓厚的学术氛围。在画中，两位古代伟大的数学家被画家安排在很显著的位置。左边方框中的中心人物是古希腊数学家、哲学家毕达哥拉斯，右边是编撰《几何原本》的古希腊数学家欧几里得。

拉斐尔，《雅典学园》

欧几里得生活于约公元前330年到公元前275年之间，被称为“几何之父”，欧几里得几何学成为用公理化方法建立起来的数学演绎体系的最早典范。在之后的2000多年间，这一严格的思维形式， 不仅用于数学，也用于其他科学，甚至用于神学、哲学和伦理学中，产生了深远的影响。

这里我们要特别提到一位著名的女数学家希帕提娅。她出生在埃及亚历山大里亚城，是世界上有记载的第一位女数学家。也另有说法，在希帕提娅之前其实也有不少女性从事数学研究，但她们的作品没有流传下来。希帕提娅的父亲赛翁（Theon）是有名的数学家和天文学家，希帕提娅协助父亲完成几何原本的现在版本，这位聪慧的女性以她的才华和贡献跻身于古代世界最优秀的学者之列。公元415年她惨死于暴徒手下。希帕提娅虽去世一千五百多年了，但她的科学精神鼓舞了一代又一代的青年人，尤其是女士们从事数学研究。今天女数学家的比例越来越高，如在世界一流大学工作的华裔女数学家就有许多。

古希腊著名数学家、哲学家希帕提娅

文献中普遍认为：欧几里得是在公元前300年左右完成了《几何原本》一书。全书分13卷。有5条“公理”或“公设”、23个定义和467个命题。欧几里得由公理,公设和定义出发，严格推导出命题。他严格论证了毕达哥拉斯定理，即“勾股定理”，从而确定了勾股定理的正确性。

远在公元前约三千年的古巴比伦人就知道和应用勾股定理，还知道许多勾股数组。古埃及人也应用过勾股定理。在中国，西周早期的商高提出了“勾三股四弦五”的勾股定理的特例。勾股定理等价于证明：在一直角三角形中，斜边上的正方形的面积等于两条直角边上的两个正方形的面积之和。

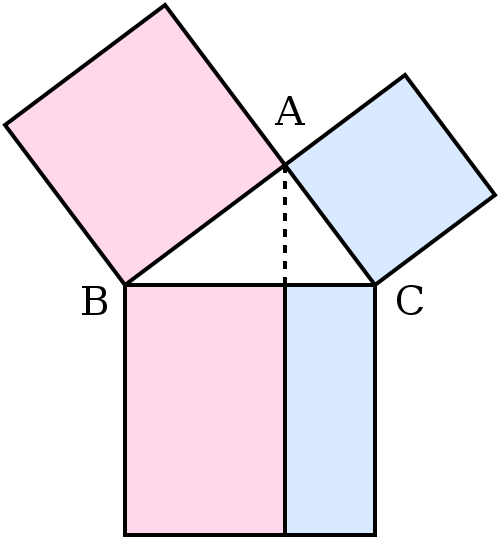
赵爽是我国数学家，他是东汉末至三国时代吴国人。赵爽为《周髀算经》作注时，解释了《周髀算经》中勾股定理，并给出了证明：“按弦图，又可以勾股相乘为朱实二，倍之为朱实四，以勾股之差自相乘为中黄实，加差实，亦成弦实。” 2002年国际数学家大会会标的灵感就来源于此，这个标志现在也是中国数学会的标志。

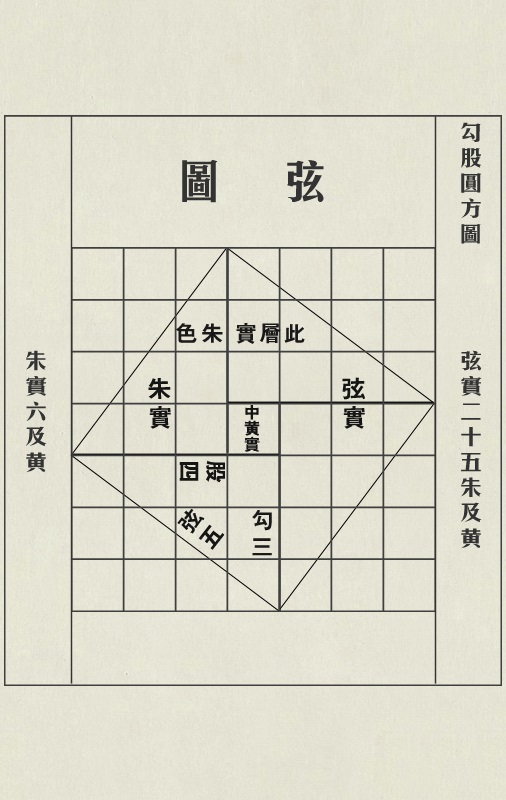
赵爽弦图

中国数学会的标志

古希腊数学家泰阿泰德发现只存在5种正多面体，不存在第6种。这一结果的证明最早也是出现在欧几里得的《几何原本》中。柏拉图的宇宙观基本上是一种数学的宇宙观。他设想宇宙开头有两种直角三角形，一种是正方形的一半，另一种是等边三角形的一半。从这些三角形就合理地产生出四种正多面体，组成四种元素。火是正四面体，气是正八面体，水是正二十面体，土是立方体。第五种正多面体是由正五边形形成的十二面体，这是组成天上物质的第五种元素，叫做以太。5种正多面体被称为“柏拉图立体”。可见被授予光环的也不一定是原本的发现者。

5种正多面体

仔细观察，城市中很多球形建筑上都有12个特殊的点，比如位于北京奥森公园附近的中国科技馆，这些球形建筑上的12个特殊点每个点由5个三角形组成，这是多面体几何性质约束的结果。大家有兴趣可以去现场找找这12个特殊点。其实，在两千多年前古希腊数学家已经发现了这一特点。

中国科技馆

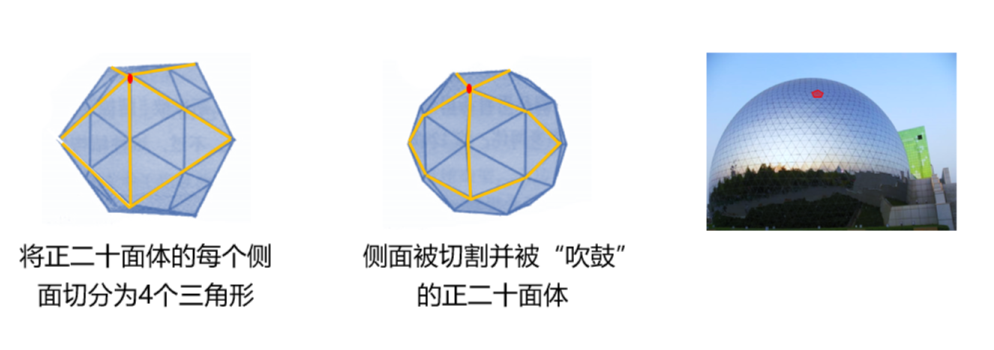
大型球状建筑物，类似于将正二十面体每个三角形切分成4个三角形，然后将每一个新的三角形再同样切分，依次切分下去，得到若干小三角形侧面，将它们“吹鼓”起来变成类球体形状。之前提到的中国科技馆球状建筑就是这样，由成千上万块小三角形拼成，球体表面的12个特殊的点就是原本正二十面体的12个顶点。在生活中，我们还可以看到类似的物品，比如足球其实是截去顶点并稍加吹鼓起来的正二十面体。

欧几里得《几何原本》中还有关于数论的结果：有无穷多个素数。素数是只能被1和自己整除的正整数， 如2，3，5，7，11，13……任何整数都可以分解成素数的乘积，所以素数被认为是数的“原子”。数论是数学的核心分支之一，研究素数是一个重要部分，许多著名猜想都与素数有关，如被誉为“皇冠上的明珠”的哥德巴赫猜想：任一大于2的偶数都可写成两个素数之和。至今最好的结果是1966年陈景润先生证明的。还有有关黎曼ζ函数的零点分布著名的黎曼猜想。素数理论被用于信息安全技术，有无穷多个素数是现代信息安全技术的基础。

素数不仅有无穷多个，我们还能描述它的分布，素数定理就是其中一个描述。素数定理（Prime Number Theorem）叙述如下：

设x≥1，以π(x)表示不超过x的素数的个数，则当x趋于无穷时，

π(x)～x/ln(x)。

1896年，阿达马和德·拉·瓦莱布桑（Charles-Jean de la Vallée Poussin）各自独立地证明了素数定理。1949年，塞尔伯格和埃尔德什（Paul Erdős）分别独立地给出了素数定理的完全“初等”的证明，这是塞尔伯格获得菲尔茨奖的一个重要工作。由素数定理，我们可以估计素数的个数，如果x是1亿，素数有300多万个。如果x是100亿，素数有3亿多个。我们还可求π(x)的渐进展开公式，第二个本质项的幂次大小与黎曼猜想紧密相关。

素数理论在好莱坞电影中也出现。获奥斯卡奖的好莱坞科幻电影《超时空接触》中就有素数理论的应用。女主人公利用素数的数学理论破译了来自外太空的密码，这些密码是生产时空机器的图纸和说明。时空机器制造出来后，女主人公成为人类首位与外星生命接触的使者，飞越宇宙，与外太空的生命进行理智的接触。

好莱坞科幻电影《超时空接触》海报

数学结论最基本的要求是“正确”，无论多么显然的结论，都需要从已知的确定结论通过正确的推理得出。这成为数学最显著的特征。几何原本提出五大公设,其中第五公设相比前四个公设不那么显而易见。那么，第五公设能否作为公设，而作为定理？循着这条路线望去，这就是最著名的、争论了长达两千多年的关于“平行线理论”的讨论。由此产生了很多意想不到的、具有重要价值和意义的研究成果。

在1830年左右，俄国罗巴切夫斯基，匈牙利雅诺什发现了第五公设不可证明，创立了非欧几何学。雅诺什在研究非欧几何学的过程中也遭到了家庭社会的冷漠对待，他的父亲——数学家鲍耶·法尔卡什劝他放弃。高斯也发现第五公设不能证明，并且研究了非欧几何。但是高斯害怕这种理论会遭到教会力量的打击，不敢公开发表。可见探索真理的道路并不是一帆风顺的，是非常艰苦的，需要持之以恒的努力和坚定的信念。

双曲几何中有四种常用模型，庞加莱圆盘模型是其中一种，如下图所示，有无穷多条线通过一个给定的点且平行于一条给定的线。

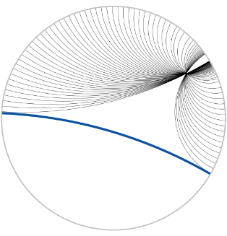
庞加莱圆盘

著名数学家黎曼1851年创立黎曼几何，引进了流形和度量的概念，证明曲率是度量的唯一内涵不变量，具有划时代的意义。从欧几里得的第五条公设引发的关注和思考，产生了非欧几何诸多重要的研究方向，这些研究都并是不以“有用” 作为研究原点的，但是最终证明是非常有价值的。1915年，爱因斯坦创立了新的引力理论——广义相对论，黎曼几何成为其重要工具。

黎曼像

数学研究的最初目的往往不是为了功利，最后却获得特别的效果和重要的应用。数学是不以“有用”为研究的原点，也就是说数学本身是非常纯粹的。好的数学并不是仅仅屈从于某个具体的目的，但是一旦取得了数学中思维的突破，实际上它却又是极为“有用”的。所以我一直都认为数学是不以“有用”为研究的原点，实际上却又是极为有用的学科，事实上，数学无处不在。下面我们一起具体来看。

数学的简洁性是人类思想表达经济化要求的反映，它同样给人以美感，给人很纯粹的感觉。爱因斯坦说过：“美在本质上终究是简单性。”比如欧拉公式，无法说清楚有多少凸多面体，但它们都必须服从欧拉公式，且由此可推出只存在5种正多面体。

多面体的欧拉公式实际是欧拉示性数的特别情形，这是一个拓朴不变量。上世纪40-60年代，示性数理论得到进一步发展， 引进了陈数、庞特里亚金数，证明了Gauss-Bonnet-Chern定理，指标定理。 这些新理论与物理中规范场论有紧密联系。在凝聚态物理中, 量子霍尔效应的拓扑序可用示性数描述。

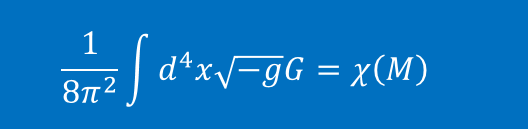
Gauss-Bonnet-Chern定理

2016年诺贝尔物理学奖颁发给三位从事拓扑相变和拓扑物质形态研究的学者。拓扑是几何学发展而衍生的一个核心数学领域，研究几何体在连续形变中所不改变的性质。拓扑物质形态用拓扑示性数，比如“陈数”，来刻画新的物质形态。拓扑相还存在于三维材料中。这些拓扑材料有望在新一代电子器件和超导体中产生应用，以及在未来量子计算机方面有应用。

对称性是数学美的一个基本内容。中国的建筑就很好的应用了数学的对称美，比如故宫在北京中轴线中心上，彰显着皇权的至高无上。走进皇城每件东西也都很讲究对称。横九路、竖九路，共是九九八十一个。对于我们中国人而言，九，是阳数之极，象征帝王最高的地位。甚至连围墙，都被精心计算好了角度。天坛也是这样，有很多对称的元素。

天坛包含了对称性元素

用形状、大小完全相同的几种或几十种平面图形进行拼接，彼此之间不留空隙、不重叠地铺成一片，这就是平面图形的密铺。除正三角形、正四边形和正六边形外，其他正多边形，如正五边形，都不可以密铺平面。但有的五边形可以密铺平面，下图列出了15种早已熟知的五边形密铺。第16种可密铺五边形是2015年由美国数学家发现的。

密铺在建筑中也常见到。西班牙格拉纳达红宫是伊斯兰世界在西班牙留下的辉煌古迹。阿拉伯的工匠们在几何图案的设计中展现出了令人叹为观止的创造力。大家可以看到，红宫的建筑纹饰是各种几何图形的对称、旋转、平移。目前存在只存在17种类型的几何密铺，我们在红宫都可以找到。

西班牙格拉纳达红宫及其部分建筑文饰

数学的深刻性是毋庸置疑的，数学中最漂亮的部分常联系着不同的分支，揭示特定的本质。比如勾股定理告诉我们：a2+b2=c2

著名的费马大定理就是记录在Arithmetica的1621年版的书中 ：如果n  > 2,  则aⁿ + bⁿ = cⁿ 没有非零整数解。费马声称自己有一个“绝妙的证法”，当然他没有写下来。

费马猜想的证明有很长的历史，期间经历了几次重大突破，这个问题最终在1994年被怀尔斯证明，他也因此拿到了为他特别制作的菲尔兹银质奖章。怀尔斯的证明用到了大量现代的数学工具和技巧，他的证明揭示了椭圆曲线和数论之间的深刻联系。

英国著名数学家、牛津大学教授Andrew Wiles

Fermat大定理的证明正是基于椭圆曲线的理论。近年来，利用椭圆曲线的密码系统越来越受到重视。椭圆曲线在密码学中的使用是在1985年由N.Koblitz和V.Miller分别独立提出的。实际上，密码学已经广泛应用在我们日常生活中，如银行密码、电子商务等。它使用了大量的数学工具。在电子商务中，经典的RSA算法被广泛使用。RSA算法是由MIT研究人员Rivest, Shamir和Adleman在1978年公开推广的，其基本原理是因为素数分解的困难。而椭圆曲线密码的安全性远高于用素数分解的RSA算法。

椭圆曲线就是三次代数曲线，即复平面上三次代数多项式的零点集，如 y^2=x^3 +1,  y^2=5 x^3–7 等。研究一般多项式零点集的几何称为代数几何。

数学的统一性可表现为数学概念、规律、方法的统一, 数学理论的统一, 数学和其他科学的统一。1904年，著名法国数学家亨利·庞加莱（1854-1912年）提出了一个拓扑学的猜想：“任何一个单连通的，闭的三维流形一定同胚于一个三维的球面。”一个闭的三维流形就是一个有界无边的三维空间；单连通指这个空间中每条闭曲线都可以连续的收缩成一点。因此庞加莱猜想可以通俗的说成：任何一个满足这样性质的三维空间，它“本质上”是一个三维的球。这个猜想可以被推广到三维以上空间，被称为“高维庞加莱猜想”。

法国邮票上的庞加莱像

多年来，每一次庞加莱猜想的突破都是数学界的大事情。1961年S. Smale证明了庞加莱猜想的五维空间和五维以上的情形，立即引起轰动。斯梅尔由此获得1966年菲尔茨奖。1982年，M. Freedman证明了四维空间中的庞加莱猜想，并因此获得1986年菲尔茨奖。很多人用拓扑学的方法研究三维庞加莱猜想没有进展，有人开始想到了其他的工具。W. Thurston就是其中之一。他引入了几何结构的方法对三维流形进行切割，提出了几何化猜想并解决了一个重要情形。W. Thurston获得了1982年的菲尔茨奖。庞加莱猜想是几何化猜想的一个特别情形，但W. Thurston解决的情形不包括庞加莱猜想情形。

千百年来，数学家们在拓展人类思维边界的道路上，不懈努力，取得了众多的杰出成果。但是还有很多悬而未解的重大问题，有待有志者去解决。比如，2000年著名的克雷数学研究所将庞加莱猜想等七个重要数学问题列为“七大千禧年难题”，即：NP完全问题、霍奇猜想、庞加莱猜想、黎曼假设、杨－米尔斯理论、纳卫尔－斯托可方程、BSD猜想。破解每个难题都可获得100万美元的奖励，这七大数学难题被认为是“对数学发展具有中心意义、数学家们梦寐以求而期待解决的重大难题”。

传奇数学家Perelman在花了8年多时间研究庞加莱猜想这个足有一个世纪的数学难题后，在2002年11月和2003年7月之间，将3份关键论文的手稿上传到arXiv.org这个专门刊登数学等学科的预印本论文的网站上，并用电邮通知了几位数学家，声称自己证明了几何化猜想。后来，Perelman理所当然地得了菲尔兹奖，但是他没有去领奖。Perelman的数学才华和特立独行，大家在网上都能查到一些描述，在这里就不再赘述。

传奇数学家Perelman

Perelman的证明中使用了R. Hamilton引进的Ricci流，它是一组微分方程。他通过完成一系列的拓扑手术，构造奇点可控的几何解，从而解决了几何化猜想以及三维的庞加莱猜想。这是用几何分析技巧理解拓扑问题的典范。

Ricci Flow

不仅数学不同分支之间有深刻的联系。数学和物理更是一直相互启发，相互推动，一同发展。爱因斯坦方程在广义相对论中，宇宙一切物质的运动都可以用几何学中的曲率来描述，引力场实际上就是一个弯曲的时空。

计数几何是代数几何的一个重要分支，研究几何方程的解的个数。它有非常悠久的历史。近三十年来，计数几何与物理的拓朴场理论研究相互影响，促进了两个学科的高度发展。它的研究更加系统化，与数学其他分支，如表示论、微分方程等紧密相连。量子同调环就是一例。1993年，受物理中场论研究的启发，我和阮勇斌首次建立它的数学理论，解决了一类经典的计数几何问题。

数学在经济学、生物学等学科的发展中也起到非常重要的作用。很多诺贝尔经济学奖得主都是学数学出身的，大家熟悉的约翰·纳什、就是数学家，也是奥斯卡电影奖《美丽心灵》的主人公原型。约翰·纳什也是普林斯顿大学教授，我之前在普林斯顿工作，在校园里时常见到他。纳什不仅获得诺贝尔经济学奖，他还获得阿贝尔奖。阿贝尔大奖是数学界的重大奖项，为了纪念挪威著名数学家阿贝尔二百周年诞辰而设立的，据说设立此奖的一个原因也是因为诺贝尔奖没有数学奖项，阿贝尔奖奖金的数额大致同诺贝尔奖相近。

约翰·纳什

此外，1997年诺贝尔经济学奖得主罗伯特·莫顿，他也是数学家。2005年诺贝尔经济学奖得主罗伯特·奥曼的最高学历是麻省理工的数学博士。2012年诺贝尔经济学奖颁发给哈佛大学教授罗斯和加州大学的沙普利，他们俩本科和博士都读的是数学专业。

数学在医学上也无处不在，如利用概率和统计来验证新药或程序的有效性，或估计接受某些治疗的癌症患者的存活率。现在我们在医院中常见的CT成像技术的数学基础是Radon变换。

CT成像技术

纯数学在遗传学的一个重要的应用是“哈代定律”。哈代是著名数学家，他曾经说过：我从未做过任何有用的事情，我的发明不会直接或间接的对改变世界作出任何贡献。有趣的是，1908年哈代的工作在遗传学方面得到了应用，并且有一个以他的名字命名的哈代定律，被称为人口遗传学的科学基础。1854年英国医生John Snow通过绘制英国伦敦的霍乱地图及利用统计方法，发现了病毒来自于被污染的水泵。近年来，研究者们综合利用统计模型，基于多源信息对传染病的流行规律进行更加精确地建模分析。此次新型冠状病毒疫情中, 国内外研究团队大多数都是以动力学模型为基础，给出疫情发展趋势的分析和预测。中国数学会已向国家提交多篇有关论文和报告。

近年来，人工智能、大数据兴起，成为受人瞩目的研究领域，北京大学还设置了数据科学专业。人工智能、大数据其实也是与数学密不可分的。有观点认为，AI人工智能科技的本质就是数学。而大数据，本质上就是海量数据的汇集，数学提供了研究基础和工具。

可见，数学有极大的价值和用处。历史的经验告诉我们，数学研究在发达国家的科学战略中始终居于最重要的地位。我们的国家要实现可持续发展必须有原创性的科学研究以及原创性的数学研究！

数学等基础学科已经得到国家重视，2018年国务院印发《关于全面加强基础科学研究的若干意见》，以进一步加强基础科学研究、大幅提升原始创新能力，夯实建设创新型国家和世界科技强国的基础。

为了落实《关于全面加强基础科学研究的若干意见》要求，切实加强我国数学科学研究，2019年7月12日，科技部、教育部等四部委联合印发《关于加强数学科学研究工作方案》。工作方案指出：数学实力往往影响着国家实力，几乎所有的重大发现都与数学的发展与进步相关，数学已成为航空航天、国防安全等领域不可或缺的重要支撑。

最后我引用四川大学罗懋康教授写的一副对联，表明我们数学家也不乏有深厚的文学和艺术修养。这副对联是：天道几何 万品流形先自守。变分无限 孤心测度有同伦。从汉语字义和数学角度去理解都充满了深刻的含义。在短短22字中，有几何、流形、变分、无限等七个数学概念。这副对联的意思是：不管客观世界的规律如何，万事万物都早已按照这些规律发展演化。客观世界的变化是无穷无尽的，总有一心追寻科学真理的同路人。数学充满着无穷的魅力，深深吸引着一代又一代有志之士不断探索、攀登。希望有更多优秀人才加入到数学研究的行列。谢谢大家！

位于北京大学全斋北门的数学对联

Q&A

问：我国中学生在世界数学奥林匹克竞赛中屡获佳绩（30多年），而至今无人获得菲尔兹奖呢？

答：奥数竞赛跟做数学研究完全是两回事。竞赛是在指定时间内解出一道给定的题目，而做研究需要自己去开发问题，对时间要求没有那么严格。从实际情况来说，我们培养一个数学人才，最重要的还是看其是否确实对数学有兴趣。很多参与数学竞赛的学生后来都不做数学了，就是因为他们对于数学并没有兴趣或是兴趣没有那么大。我们现在有些年轻数学家确实做出了非常突出的工作成果，至少是有可能得奖的，但是否近几年内就能拿到，这很难说。就像是张伟、恽之玮、许晨阳、还有朱歆文都做出了相当好的工作。我也知道我们现在有一些年轻人也是积极努力朝这个方向走，获奖就是一个时间早晚的问题。 获奖与否也取决于很多因素，评审委员会也是来自各个国家，候选人的工作成果也需得到国际学术界的了解和认可。我们会为年轻学者创造更好的条件，鼓励他们做大问题，参加一些重要的学术交流，争取更多的国际认可。当然，比起得奖，对数学发展来说更重要的还是产生一些对人类的发展起到关键推动作用的工作。

问：接触一个相对新的数学领域，尤其是对于新人，有什么好的建议吗？是读一本这个领域的著作，还是读几篇或者十几篇高质量的论文？如何效率高一些？

答： 打好基础对学习新领域是非常重要的，开始的时候可以先读一些相关领域的书籍了解基本概念，这个是必要的。再根据兴趣读一些论文，当然论文不像书籍那样一层一层的条理非常清楚，论文思维上可能会有一些跳跃，读起来有难度，初学的人不要感到很为难，不强求读得多，根据个人兴趣和情况，可先挑选一些重要的文章阅读。可以通过设法推广延伸，深入理解论文的结果和方法，多思考，努力解决一些问题，做研究一定要有耐心，不必太过担心效率。

问：怎么样让中国数学从小学开始培养，小学生如何建立数学思维，家长在家庭生活中如何有效引导孩子（当然不仅仅是学习书本）

答：（笑）这个问题可能是家长提的。刚才我在报告中也介绍了，其实数学离我们日常生活并不遥远，数学无处不在，在自然界中有数学，在日常生活中到处都能找到数学的影子。在家庭教育中，孩子的数学思维培养可以从生活的小事着手。比如孩子很小的时候让他对应着实物数数，建立起数字的概念。比较大小、长短、高矮等等，在孩子脑海中建立抽象概念。另外，平时也可以与孩子玩一些有趣数学的游戏。我的母亲也是数学家，我记得在我小时候，那时候物质条件远不如现在，我母亲就和我玩称球游戏，给定球的数量和限定称的次数，找出坏球。通过寓教于乐，孩子不会觉得枯燥，培养了孩子的好奇心和求知欲，帮助他们建立起逻辑推理的能力。现在有很多学习机会，如科普书籍和网课，可以有针对性地选择一些数学启蒙书籍对于建立数学思维也是很有帮助的，比如我母亲在我小时候就引导我读几何原本，那个时候我对数学产生了浓厚的兴趣。

问：来自辽宁-营口的网友：您认为目前中国基础教育的数学发展中的优势在哪里？还有哪些有待进一步深入推进的方向呢？

答：这十几年来，中国数学有了非常好的发展，尤其从国家的各大人才计划实行以来，引进和培养了一批非常优秀的年轻人，对数学的队伍建设起了非常好的作用。随着国家的经济条件变好，高等教育水平的提高与学校人才培养质量的提升，以及现在国家对数学的重视，年轻人学数学的热情和兴趣也提高了，人才后备军还是很不错的。这几年我们确实培养了一些相当好的年轻人。整体来看的话，中国数学的发展趋势还是非常好的。但在一定程度上，如果在三四十岁以下的年轻人中间比较，中国的数学人才和美国或是整个欧洲还是有一定差距，但是要是和欧洲某个国家相比，我们还是有一定优势的，因为确实有一批优秀的年轻人，而且中国人也多。和美国相比的话，美国的优秀人才的来源更丰富也更多元，因为它把全世界优秀的人都吸引过去了，而我们目前主要的人才来源还是集中在华人或者是归国的人才，还有靠自己培养的一部分人才。但是我对于以后的发展还是充满信心，主要是我们的队伍比较好，当然可能还需要一些时间让外人来了解我们所做的工作，再通过一定的努力可以吸引到一些国外的好的学生或是博士来中国学习、工作，以扩大我们的国际影响。当然，一所大学或者科研机构是否真的达到世界一流，其中一个重要的标准是看世界各地的年轻人是否愿意来这里学习。对于博士或是博士后来说，他们不会只考虑待遇的问题，他们更看重在这里的经历对他们以后的发展有没有帮助。在这个方面上，我们的条件也是越来越好了，有一定的竞争力，但是还是需要继续努力。